Day 5: A Quiz, Special Right Triangles and Cups

Day five.  The first Friday.  My students were tired.  I was tired.  The first week was successful; at least, I felt that it was.

AP Statistics: The first week culminated in a quiz.  I did learn that we need to work on communication through writing.  I feel like they have a good grasp on what we’re learning, but they’re having trouble communicating it.

Precalculus:

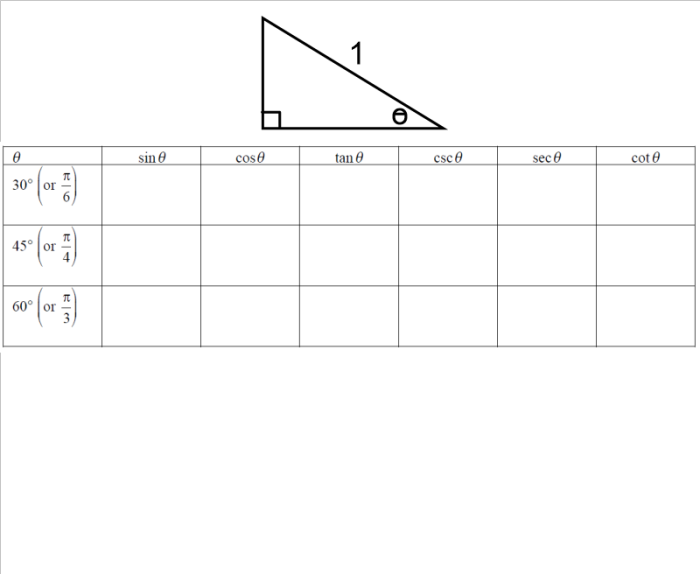
In precalculus, today’s lesson is to connect calculating trigonometric function values with their knowledge of special right triangles.  I was a bit concerned about their memory of special right triangles, so their warm up had them working with 45-45-90 triangles:

My hope was that they’d quickly realize the pattern that the length of the hypotenuse is the leg times the square root of two.  They did, and they had the “oh yeah” moment.  I regret not proving this fact to them.  I need to make sure when we’re coming up with rules and theorems that I’m more formal about it; those students who go on to do higher mathematics need that exposure.

After spending time with 30-60-90 triangles, the end of class culminated in:

The part my students are struggling with the most is the simplification of fractions with square roots.  I’m trying to convince them that they’ll become comfortable with them; they just need to be willing to practice.

Algebra II Honors:

I’m a bit concerned that my students don’t know what makes a linear function linear.  We took a day out to discover what linear really means.  I’ve told them that as we look at functions, we’re going to study them in three ways: a graph, a set of coordinates, and an equation.  They knew what makes a graph of a function linear, but not the other two representations.  So we explored:

Each pair of students received three cups and a ruler.  From that information, they needed to make their estimation.

In case you want to play along:

Most groups realized that there is a constant growth in height caused by the lip of the cup.  From that measurement (which is really 1.5ish centimeters…even though it looks like 2 centimeters in the picture) they extrapolated their guesses.

A few groups got to 116 cups.  Most were within 10 cups.

From their realization that the height of the stack grows at a constant rate in relation to the number of cups, we had the discussion of what linear means.  Ideas about rate of change, y-intercepts, and functions were all discussed.  The hope was this concrete example would let them see that constant change (slope) is what makes a function linear.  This led to other discussion and playing with geogebra.  Fun was had by all (or at least me)!

AP Statistics: The Law of Large Numbers

I’ve been trying to come up with a way to immerse my students in the law of large numbers without simply giving them the law and reading example after example.  To jog your memory, the law of large numbers states: as the sample size increases, the experimental probability will approach the theoretical probability…or as one of my students stated, as the sample size gets larger, the prediction (experimental probability) gets more accurate.

I’ve been playing Pass the Pigs for a long time, and I’ve always wondered about the probability of having the pigs land in the different piggy positions. (If you don’t know what I’m talking about, go here: http://passpigs.tripod.com/rules.html).

So, I asked them this question:

I explained to my students that we were going to modify the game to just look at rolling one pig.  The conversation started with my students deciding that the higher the point value, the harder that type of roll is to get.  someone eventually made the connection that the difficulty of the roll is inversely related to its probability.  I then asked them what the probabilities for the different rolls were.  They didn’t know,but were willing to roll some pigs to make some predictions . After some rolls, we gathered the class’s data and calculated experimental probabilities:

Tons of great conversation followed.  They argued about fairness and attempted to come up with a point system that was “fair.” After a few minutes, I brought them back to see what they were doing.  I pointed out that they were using those experimental probabilities as if they were the absolute truth.  A student quickly quipped: “but we did a lot of rolls, it should be pretty accurate.”

Then, and only then, we discussed the law of large numbers.

How Much is This Cheeseburger?

We have reached spring break. This past Friday, we had our school’s spring carnival. This meant that teachers lost a day with 6th and 7th periods. My Algebra II classes are 4th and 7th period; so I didn’t have class with 7th period on Friday. Since we had just tested the day before in 4th period, I decided Friday was a perfect day to experiment.

The first day of class in my classroom changes each year. I always start the year placing my students in a mathematical situation. While it may not be directly from the curriculum, I feel that my students can get the best idea what my class is about by doing math…as weird as that sounds. Placing them in the thick of a math problem and see how they respond gives me a lot of information about my students. Likewise, being in the thick of a math problem can tell my students a lot about what I expect of them.

My 4th period class likes to be a challenge. They don’t like math/ think math is hard/ just want me to tell them what to do so they can move on with their lives/ are tired of the school year and are looking forward to summer (and probably summer 2015 for a bunch of them). This mindset is perfect for my experiment.

So here’s the experiment:

What a simple question. How much was that cheeseburger. There tended to be two common responses: “ewww” and “I want one.” Then the guesses started flying. Some were reasonable, some definitely weren’t. I didn’t care about the unreasonable guesses; at least they were engaged in the question and were taking some ownership in the problem. Finally some questions were asked. The most important questions got me to tell them that on this burger there was one bun, one hundred patties, and one hundred slices of cheese. Now the question is accessible. “Give us some prices Mr. Cloud.”

So I did:

That’s all they get. That’s all the menu at the restaurant has. There weren’t any complaints. Nobody said this is stupid. They went right to work trying to figure it out. There were wonderfully insightful conversations/questions. “A cheeseburger has one bun, one patty and one piece of cheese. You can’t just multiply by 100. You’ll have 100 buns.” It was a magical 15 minutes. I didn’t have to lead or quiz or scold or encourage. They were doing it; they were doing math. They were discussing and justifying. Groups started collaborating with other groups. They were getting the same answer. Groups that didn’t get it asked for explanations from other groups. All of this from a group of students who couldn’t care less (at times) how the fundamental theorem of algebra relates to the real and imaginary roots of a quintic polynomial. This lesson worked and will work as a way to create a setting for next year’s classes. Now just to figure out how to do this every day. This 15 minutes is how I picture my classroom all 50 minutes all 180 days.

Oh here’s the answer by the way:

Somewhere in the neighborhood of 95% of my students got to the answer. They used systems of equations and didn’t even know it!

So here’s the first post of many that will give insight into the delights, horrors, difficulties, and payoffs to creating math curricula that will stretch my abilities as a teacher and my students’ abilities as, well, students.

I’m planning, no…I’m going to create lessons that create curious and excited math students in geometry, algebra II and statistics. I’ve starting developing some ideas and it’s hard to do. Darn hard. But it needs to be done. It needs to be done for the sake of my students.