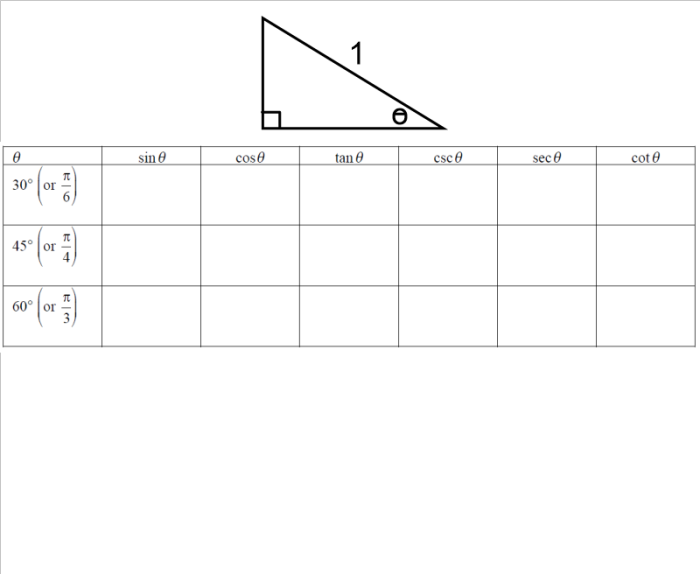
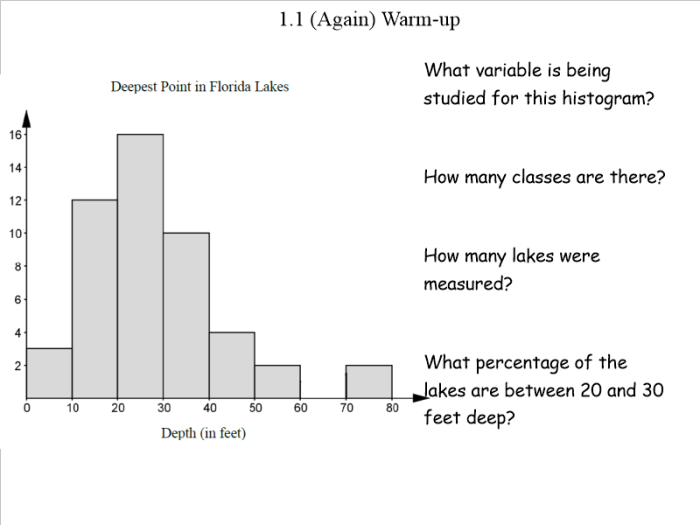
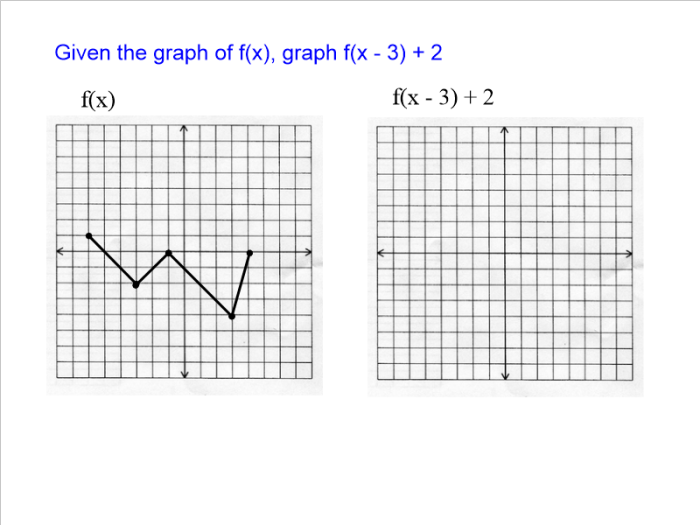
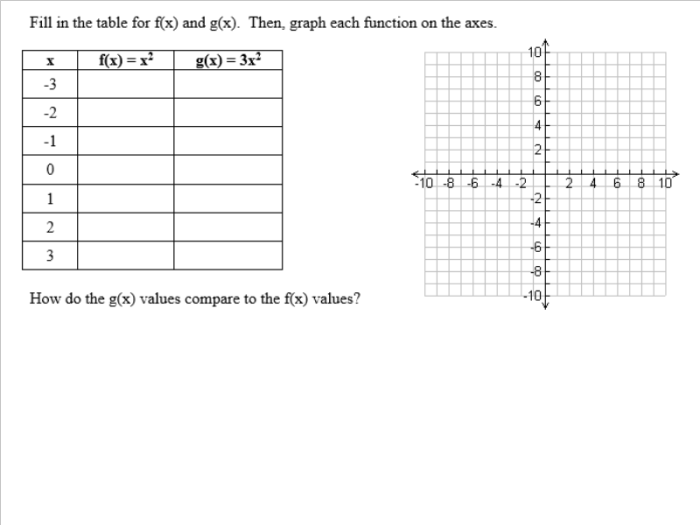
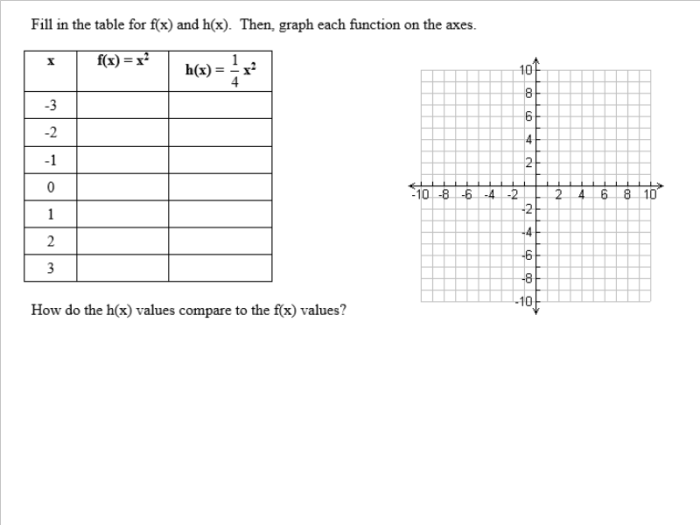
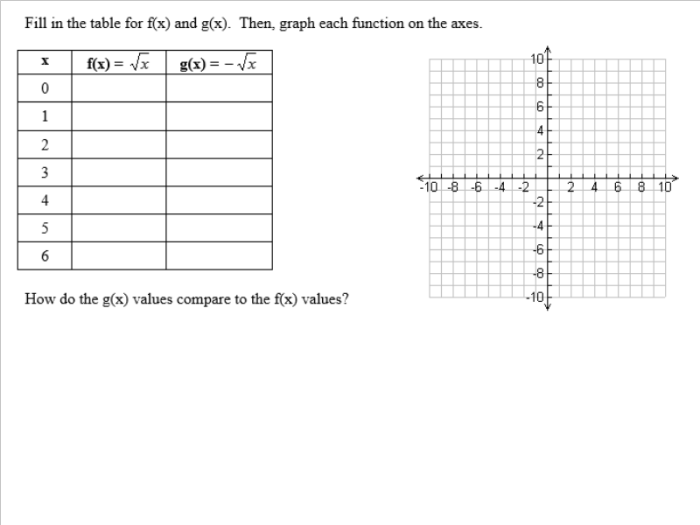
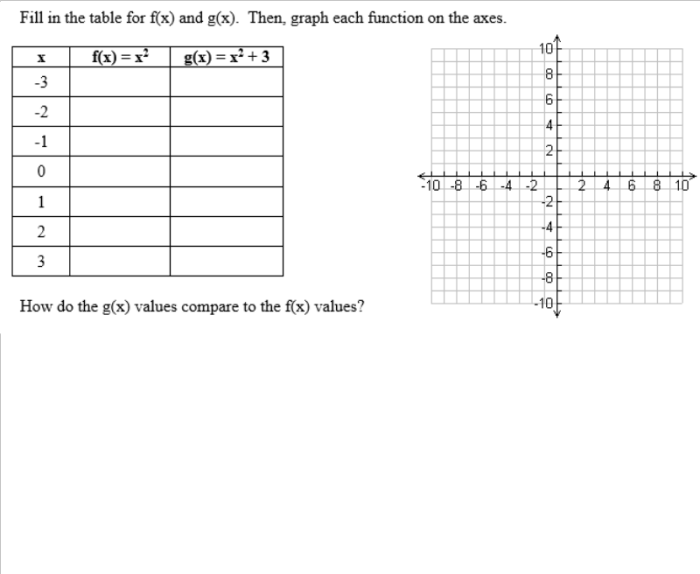
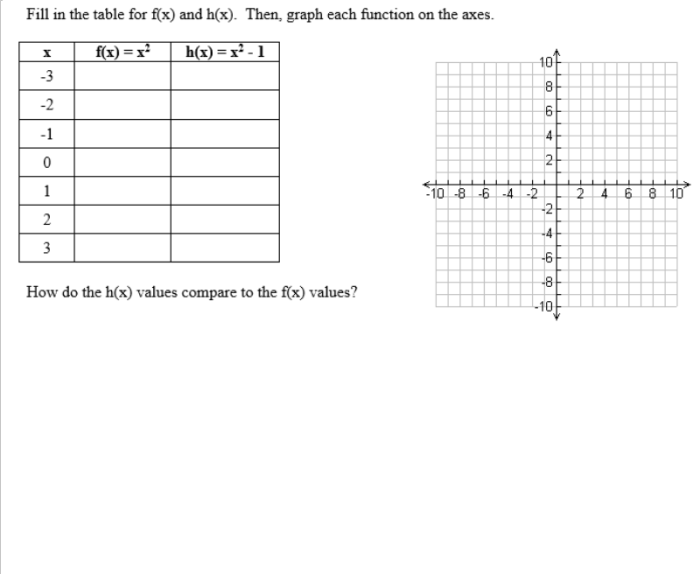
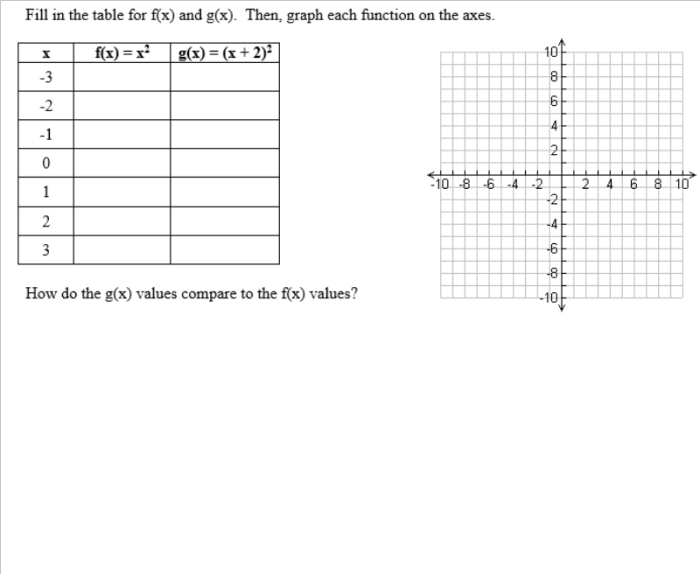
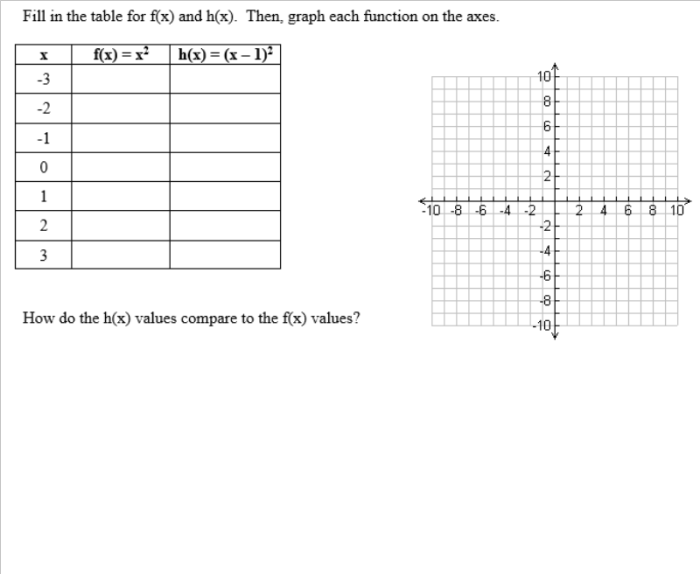
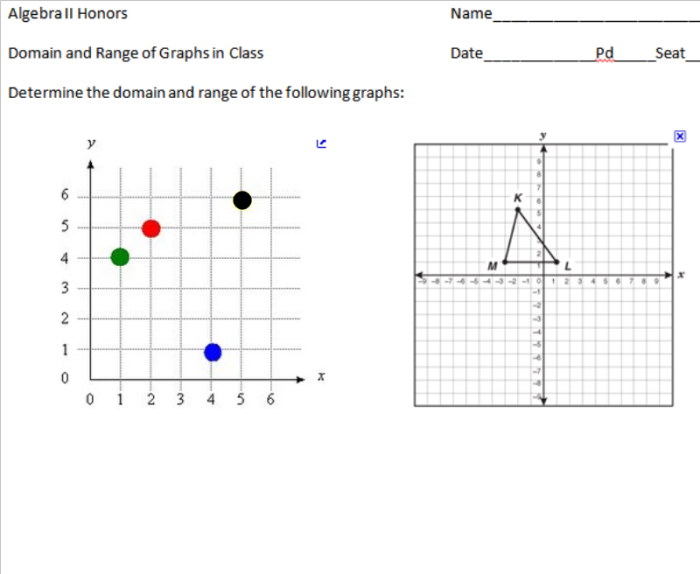
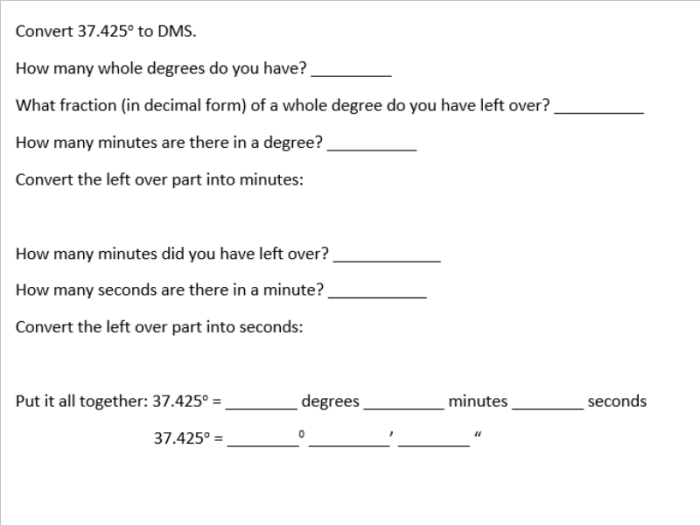
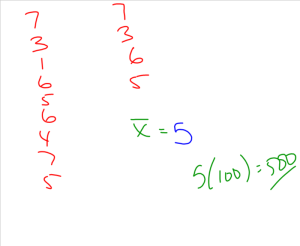Well, I’ve started planning some activities/interesting questions to add to my AP Stats curriculum. I’ve noticed that my teaching lacks the ability to have my students see the normal distribution happen naturally. Every year, I’m forced to have my students take my word that the normal distribution is…well…really real.
So, seeing that I’ve had some time to develop some lesson ideas (which is code for I get to watch The Price is Right)…and I remember seeing this:
Note: I’m going to come up with some binomial distribution lesson from this video too
I’ve taught workshops for teachers that involve probability, the normal distribution and the mention of galton boards (go ahead and click it…I made the hyperlink). But the mention of the galton board was just that…a mention. I wanted to have my students experience it!
I scoured the internet for an inexpensive (it is the summer afterall) galton board. No such luck. I tried to find a video on the internet that I could pull data from. Even less luck. So I made my own videos.
This is meant to be a ten minute #threeactmath inspired (gotta love Dan Meyer) activity.
It starts with:
Then, after some class discussion, they’ll find out there a total of 500 balls dropped. Their job is to predict what will happen.

The hope is to start making connections between the shape of the distribution and probability. There are more ways to a middle slot than an end slot; meaning that there should be more in the middle. The distribution should be symmetric (and we’ll discuss what would make it not symmetric). Basically, building the idea of unimodal and symmetric for a normal distribution.
Then they’ll finally see the answer:
More than likely, my students won’t be correct in their guesses, but the conversation is really the important part. I’m hoping to bring this back when we talk about binomial distributions/probability as well. The more I write about this, the more I realize there’s some really rich discussion can come from this.
Please feel free to comment and discuss any thoughts you have.