How Far Does Mr. Cloud Have to Run

I wanted to give my students a way to define an angle of depression for themselves. I found an interesting context involving finding a vertical distance given a horizontal distance and an angle of depression. I found it easier to switch which piece of information I gave them, but it’s practically the same idea.

The weather here today is pretty terrible. It’s been raining, is raining and is supposed to continue to rain. So I used that as the opener:

Then, I gave them the situation they were to work through:

Then came the question:

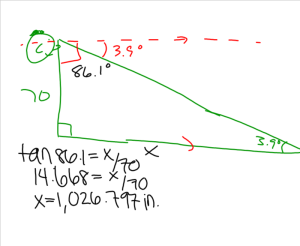
The students gave their guesses and we were off. A student pretty quickly gave the idea that a triangle would come in handy and two other students asked for my height and one of the angles (you’d think we’d been doing trig ratios in class all week).

Getting the students to figure out what the angle I gave them represented in the picture was harder than I anticipated. I had a student tell me it was the angle from the other side of the courtyard to my eye line was the angle (which is equivalent) but couldn’t tell me why.

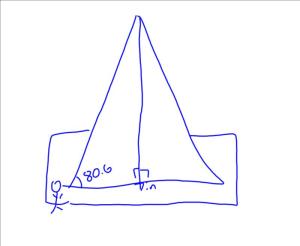
Once we figured out what the angle was on the picture, we ended up here:

Overall, we came to the definition I wanted and each group did well in working the problem out, but this problem too quickly turned into an exercise with pretty pictures rather than a great discussion about angles of depression. I’ll have to tweak this one next time.

How Tall is My Cone?

I guess I should start with the cover photo for this blog.  I have taken a Dan Meyer (look him up if you don’t know who he is…it’s definitely worth it) idea and have started using application problems as a way to get my students involved in doing math.  Not doing problems, but doing math.  I found a good trig problem involving a pyramid ruin in Egypt.  The top was missing and the students were given the angle of elevation for the pyramid and its distance from the center to the edge (including a picture with the right triangle already drawn).  That problem was the basis for this:

 

I started with a question and a teaser:

I had the students guess how tall the cone is and I also had the students guess how I was going to have them solve it. I’ve found that guessing is the cheapest and easiest way to get a student to buy into a lesson.

Then came the real problem:

I had and still have the cut base of the cone for them as a visual. Next came the student asking for information. I will not give them any information about the problem without them asking for it.

Then the students had a chance to work with the information they asked for. They worked in pairs and we came back together as a class and started to try to figure out what to do:

This was the work of one of the students. And this is when the bell rang. Their homework was to finish the problem. The students got an answer around 20 inches. I then showed them the answer:

Then we had a discussion about why thier answer wasn’t correct. Someone finally made a point about they didn’t add the base in (but that only made their prediction worse). After some deliberation, someone relaized that we calculated the height as if the top of the cone came to a point. Turns out, it doesn’t. Someone came to the board and extended the cone with two line segments and decided that’s why they were a couple of inches off.

There could be an interesting follow-up when we get to solids!

So here’s the first post of many that will give insight into the delights, horrors, difficulties, and payoffs to creating math curricula that will stretch my abilities as a teacher and my students’ abilities as, well, students.

I’m planning, no…I’m going to create lessons that create curious and excited math students in geometry, algebra II and statistics. I’ve starting developing some ideas and it’s hard to do. Darn hard. But it needs to be done. It needs to be done for the sake of my students.