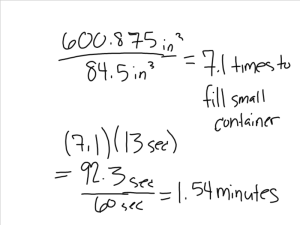Mr. Cloud Likes to Run

In geometry, we started a unit on angles and segments in circles. Since we are at the end of the softball season, I decided to use a situation that I’ve encountered to help them figure out how to calculate arc length.

I like to work out and run during the hour I have after school and before needing to be at softball to start pre-game warm ups. In order to save some time, I usually run around the school or on the softball field. So the question arises:

I define a pole as from the left field foul pole to the right field foul pole and back. My students immediately asked for some measurements and some sort of “proof” that the field was circular.

My students quickly figured out that the 90 degree angle made by the foul lines was a quarter of the circle and tied that to the idea that they were using a percentage of the circumference. As a group, we came up with a general formula and then worked some practice problems dealing with arc length.

Follow That Yellow Brick Road

During the past few years of teaching Algebra II, I have found that teaching students to recognize and understand the different types of discontinuity in a function is quite difficult. I’ve found it even more difficult to have the students discover the different discontinuitites for themselves. This year, I decided that a Wizard of Oz analogy was the way to go. Here’s what I want my students to be able to work with:

And here’s what I set up in the front of my classroom:

The idea is that the path is not continuous (my students determine this for themselves based on their definition of continuous that they develop for the warm-up to this lesson) and I have booby-trapped the path with each type of discontinuity for them to discover and define.

Removable Discontinuity:

Notice that brick 3 is conveniently missing. My students were quick to notice a discontinuity. I asked them to describe what happened and to name the discontinuity. With some probing, they got to the idea that the brick has been removed and they coined the term “removable discontinuity.”

Jump Discontinuity:

In each of these cases, none of the bricks are removed, they’re just not part of the same path. My students were quick to notice this and decided that these aren’t removable discontinuities. Since they had to jump to get from brick 6 to brick 7, they named this discontinuity “jump discontinuity.”

Asymptotic Discontinuity:

My students thought they were at the end of the road when they got to brick number 12.

However, I told them that there’s a brick 14 in the next room.

Since we had spent some time recently discussing asymptotes and how they apply to exponential functions, my students quickly figured out that the wall represented an asymptote and that we had an asymptotic discontinuity.

This path will stay on the floor of my classroom for me to refer back to when we discuss any discontinuities of rational functions. This way, I hope that they can have a meaningful way to connect something abstract in an equation or graph to their definition of each discontinuity.

Mr. Cloud Makes Dinner Part 2

So yesterday’s and today’s lesson in geometry started with this picture:

The question asked of them was “Will the pot of sauce overflow when the meatballs are added?” My students were quick to break that question down to “how many meatballs will make the pot overflow?” They’ve gotten to the point that they ask for measurements very quickly:

They had their dimensions. Then they asked for the sauce level:

They knew that we’ve been working with volume, but we had not discussed cylinders yet (they were at least calling the pot a cylinder). They asked about how to do the volume of a cylinder and that turned into a 30 minute lesson involing some basic calculus ideas. The bell rang and they didn’t get their answer.

Today’s lesson started with a review of the homework from the previous night. Once they felt grounded with cylinders, we brought back up the measurements. They calculated their volume of the pot. They quickly realized that the meatballs are spheres. On went a lesson about the volume of a sphere. Once they were okay with that, we got some measurments:

I didn’t give them every meatball’s diameter, but they decided that 4.5 cm was a “good enough” estimate (they actually found a use for an average). Then came their work:

The general consensus was that 11 would be okay but meatball #12 would be too many. Tomorrow we get to see if they were right!

Is Our School’s Kicker Better Than A Professional?

I have the luxury, nay, the honor, of teaching the high school varsity kicker in my statistics class. He’s been talking about how good he is, and I wanted to give him the chance to show off. We are learning how to run significance tests for proportions and I decided to take a different approach in how we addressed the topic. I didn’t tell my students about what new significance test we were learning, rather, I just gave them this:

The kicker’s picture has been removed for obvious reasons. The slide did not have any of the writing on it; we added that as needed during the lesson. I asked my students how we could answer who was a better kicker. The first thing they decided was that they needed to see our kicker in action.

I asked him to kick ten field goals from 40 yards. 9 out of 10 isn’t bad. Definitely better than I would ever do. Then my students wanted to compare what our kicker did to the professional. I was ready for them:

We spent some time dissecting the statistics and decided that the only important value was that the professional was a 0.729 career kicker from 40-49 yards. A lot of great conversation came from whether this was a fair comparison, what stats were relevant, could we treat this as a population value, etc.

We started running the significance test, and my students led me through what should happen. They made the hypotheses, decided they needed a proportions test, figured out that a binomial distribution applies, and ran the test.

They figured out that the sample size that our kicker kicked wasn’t large enough for us to draw any usable conclusions (and I set that up on purpose). My students were so into it that they asked how large of a sample size was needed to draw valid conclusions.

I wasn’t expecting them to ask that questions, but loved that they did. They took ownership in the problem and drove the conversation themselves. All I did was guide the conversation and point out what they already knew!

How Long Until Mr. Cloud’s Out of Water?

Today in geometry, I had an empty 2.5 gallon container of water. I raised the question “How long did it take for me to drain the container?”

The first step was for the students to decide what was a reasonable guess:

Once it was time to get to mathematical business, they quickly asked for some measurements. We’ve just started with calculating volume, so they decided for length, width, and height:

There was a quick conversation about the water level at the start of the draining, and a quick conversation about the accuracy of our calculations since the container isn’t a perfect rectangular prism.

Finally, someone asked how fast the water drains out of the container. I couldn’t answer that question for them, but I could give them this:

It took me 13 seconds to fill up the smaller container. My students were content at this time and went about their calculations. Most of the calculations were along these lines:

Seemed reasonable. Most people were in this ballpark. So we got our answer:

This confounded them. They weren’t right. They looked to me for answers. No calculation errors were found. They concluded that the flow rate wasn’t constant and that the amount of water in the container helped determine how fast the water comes out. Huge insight!! Now if only we offered physics!

Mr. Cloud Cooks Dinner

My wife was going to be late getting home from class and I was on my own for dinner. I was going through the fridge and noticed that it was time for a cleaning. We had some veggies and such that weren’t quite in a condition to eat…so I thought that it was a perfect opportunity to make a geometry lesson on cross sections!

The idea is for students to have to give their best interpretation of what they think the cross section of each cut would be. This lesson isn’t anything too special or ground breaking. Just a nice twist to give my students a real-world look at what cross sections are and how they’re already familiar with them.